
Like many things that we teach, math can feel very abstract and out of touch. The goal is always to find a way to make math skills, and any skill, more concrete. Specifically, for math, we have an advantage because it is so easy to grab a few good manipulatives and really model, practice, and create various math situations.
One of my favorite strategies has got to be using linking cubes in math. Its versatility is unmatched. Students can use linking cubes as math manipulatives to both solve math problems and understand what they truly mean.
As students actively engage in manipulating the cubes, you garner an active learning environment where students can easily see the results of their solutions and correct any mistakes immediately, fostering an even deeper understanding.
Linking cubes help students understand number bonds thanks to their easy-clicking nature! It’s easy for students to build and break apart numbers using these simple manipulatives.
For example, using a large number bond template for practicing part-part-whole relationships, students can use linking cubes to build addition problems. They can model each part of a number in the part section and then students will move those parts into the whole section.
This is an ideal whole-class activity that you can use to show students how to find the part-part-whole and build a sound foundation for mental math.
Measurement is a skill that requires hands-on practice. Linking cubes are the perfect tool for introducing nonstandard units of measurement. What I love about using linking cubes as a beginner nonstandard form of measurement is how easy they are for students to work with and line up so they can see the units change.
For example, students can measure lengths and widths by simply lining the cubes along the edge of various objects. Give students a set of objects or images of objects, and they can use a recording sheet to jot down the number of cubes they used.
In addition, students can practice ordering the objects by height or width and use their measurements to confirm. By comparing the lengths of different objects using linking cubes, students can understand concepts such as longer, shorter, taller, and smaller.
This linking cube activity is a wonderful way for students to grasp the concept of measurement before moving on to traditional units like inches and centimeters.
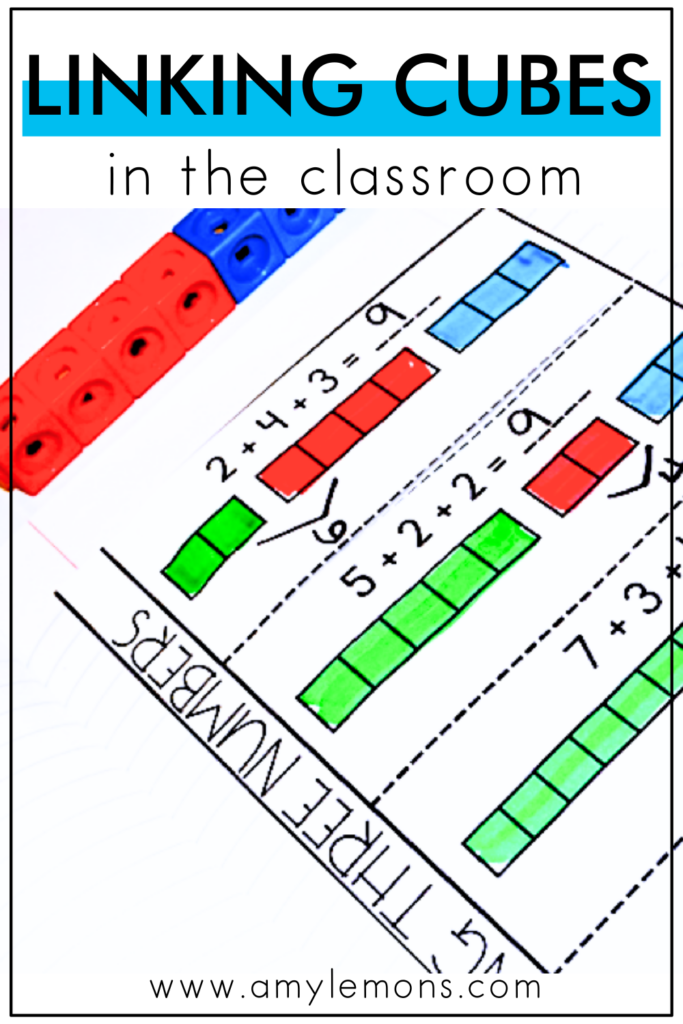
Traditional addition of two single numbers is already a huge jump in student math skills, but add in a third number and we’ve got a tricky concept on our hands!
Luckily, these linking cubes are an easy solution to teaching students how to add three numbers. An effective way to show students how to combine numbers is by snapping linking cubes together and making physical representations of the numbers.
For example, the teacher gives students an addition work-mat that shows various equation situations with three numbers. Using their linking cubes, students can learn how to combine the numbers in different ways to find the sum by simply snapping the cubes together. Also, they learn that you can change which two addends you add first and the sum stays the same.
This is great practice for using the associative property of addition.
Addition isn’t the only math skill made easy using linking cubes. Teaching students subtraction using these tools is another brilliant method. Breaking apart linking cubes is even more thrilling than snapping them together! Instantly, students are all in on the lesson.
Thanks to this simple hands-on approach, they can experience the physical act of breaking apart or taking apart numbers—which is required with subtraction.
For example, in the pictured Build and Break Activity, students will model subtraction by creating a tower of a certain number of cubes and slowly breaking it apart using subtraction. Here’s a little step-by-step of how to engage in this activity:
As students remove each cube, they can count backward and have a concrete understanding of how to subtract or break apart numbers.
Much like addition with 3 numbers, adding multiples of ten is a whole new ballpark for students. Students must understand the separation of tens and ones and how to view multiples of tens as groups of tens.
Linking cubes can help students see that adding multiples of ten involves combining whole groups of ten by using linking cube “trains”.
For example, you can begin by modeling how to build two-digit plus one-digit addition problems. I like to use large numbers to help with the visualization as students build the two numbers with cubes.
Instruct the students to place the linking cubes right beside the addition problem vertically so they can see that tens should be lined up with tens and ones should be lined up with ones. This helps emphasize to students that in addition there are two parts and you are going to combine them to form a whole.
The activity helps strengthen students’ understanding of place value and eventually transition from concrete manipulation to abstract thinking.


Hey, y’all! My name is Amy Lemons and I am passionate about providing students with both engaging and effective standards-based Math and ELA lessons.

Sample a day of Rooted in Reading with these lesson plans and activities for Reading Comprehension, Vocabulary, and Grammar!


